This Calculus Problem of the Week focuses on computing limits. We guarantee that you will have exam questions very much like these, and so we encourage you to practice many of the various types so you’ll be fully ready.

Detailed Solutions

(a) Use Factoring to Find a Limit

\(\displaystyle{\lim_{x \to 2}\dfrac{x^2 + 3x-10}{x-2} = ?} \)

We of course try Substitution first:

\begin{align*} \lim_{x \to 2}\frac{x^2 + 3x-10}{x-2} &\overbrace{=}^{?}\frac{(2)^2 + 3(2)-10}{2-2} \\[8px] &= \frac{0}{0} \end{align*}

The $\dfrac{0}{0}$ result is “indeterminate,” which is a fancy way of saying we have more work to do to actually find the limit: we can’t conclude anything from this move alone.

In fact this is a classic “factor to find the limit” problem, which is the type that appears most frequently on exams. You can practice many more of them (all free, and each with a complete solution one click away) on our Factor to Find a Limit screen. The key take-away is clear: if you can factor the numerator and/or denominator, do so. Here, we factor the numerator:

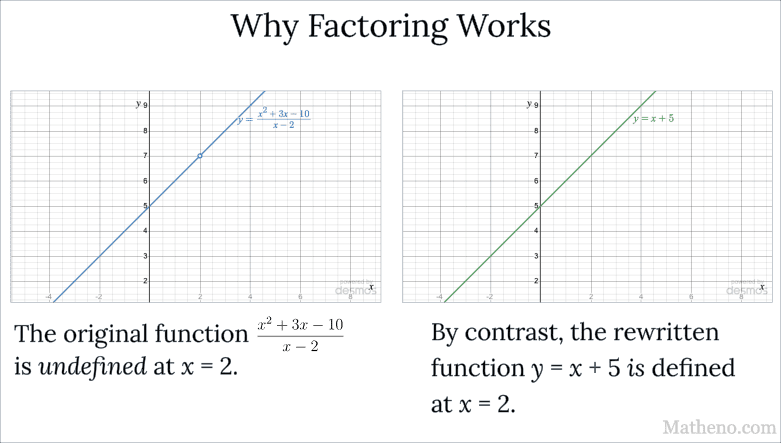
\begin{align*} \lim_{x \to 2}\dfrac{x^2 + 3x-10}{x-2} &= \lim_{x \to 2}\frac{(x-2)(x+5)}{x-2} \\[8px] &= \lim_{x \to 2}\frac{\cancel{(x-2)}(x+5)}{\cancel{(x-2)}} \\[8px] &= \lim_{x \to 2}(x+5) = 7 \quad \cmark \end{align*}

This will always happen: after you factor you’ll be able to cancel some terms, and can then use simple Substitution to finish. As we discuss on our “Factoring” screen, this tactic works because we’ve rewritten the function in an equivalent form, with the exception that while the original function is undefined for $x = 2,$ the rewritten function is defined for that input value.

The two functions thus are not identical, but we have a handy theorem that tells us that the limits are the same:

More problems to try, and further discussion of why the tactic works, are in the Topic Factor to Find a Limit.

(b) Use Conjugates to Find a Limit

\(\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x}=?}\)

We again first try Substitution:

\[\lim_{x \to 0}\frac{\sqrt{x+5} – \sqrt{5}}{x} \overset{?}{=} \frac{\sqrt{0+5}-\sqrt{5}}{0} = \frac{0}{0}\]

Since the limit is in the form $\dfrac{0}{0}$ , substitution again gave an indeterminate result and we again have more work to do.

This time we must rationalize the expression, which is our second crucial tactic. We have more discussion and lots of practice problems on our Use conjugates to find a limit screen.

The tactic is to use algebra to get rid of the square roots: we multiply both the numerator and denominator by the conjugate of the numerator, $\sqrt{x+5} + \sqrt{5}$. We can do this since we are multiplying the original expression by $1= \dfrac{\sqrt{x+5} + \sqrt{5}}{\sqrt{x+5} + \sqrt{5}},$ which doesn’t change the value of anything.

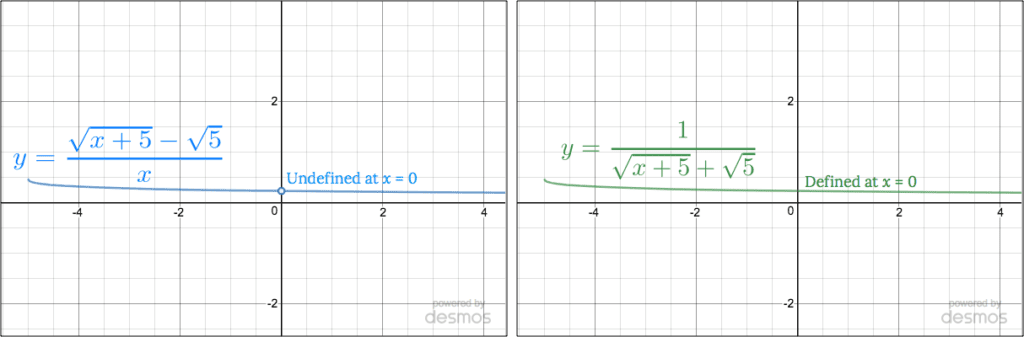
\begin{align*} \lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} &= \lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} \cdot \dfrac{\sqrt{x+5} + \sqrt{5}}{\sqrt{x+5} + \sqrt{5}} \\[8px] &= \lim_{x \to 0}\dfrac{\sqrt{x+5}\sqrt{x+5} + \sqrt{x+5}\sqrt{5} – \sqrt{5}\sqrt{x+5} -\sqrt{5}\sqrt{5}}{x\left[ \sqrt{x+5} + \sqrt{5}\right]} \\[8px] &= \lim_{x \to 0}\dfrac{(x+5) – 5}{x[\sqrt{x+5} + \sqrt{5}]} \quad\color{blue}{\text{[Notice we have not multiplied the denominator terms together…]}}\\[8px] &= \lim_{x \to 0}\dfrac{x}{x[\sqrt{x+5} + \sqrt{5}]} \\[8px] &= \lim_{x \to 0}\dfrac{\cancel{x}}{\cancel{x}[\sqrt{x+5} + \sqrt{5}]} \quad\color{blue}{\text{[… because then the $x$ then cancels nicely here.]}}\\[8px] &= \lim_{x \to 0}\dfrac{1}{\sqrt{x+5} + \sqrt{5}} \\[8px] \end{align*} Once again we can now use Substitution to finish: \begin{align*} \phantom{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x}} &\phantom{= \lim_{x \to 0}\dfrac{(x+5) – 5}{x[\sqrt{x+5} + \sqrt{5}]} \text{[Notice we have not multiplied the denominator terms together…]}}\\ &=\dfrac{1}{\sqrt{0+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} \quad \cmark \end{align*} Similar to what happened with our factoring problem above, the function we started with,  $\dfrac{\sqrt{x+5} – \sqrt{5}}{x}$,  and the one we ended up with (after multiplying by the conjugate),  $\dfrac{1}{\sqrt{x+5} + \sqrt{5}}$,  are the same everywhere except at $x=0,$ where the original function is undefined but the rewritten function is. Hence their limits are the same.

By the way, notice what we called out in the blue text in the equations above: when we multiplied by the conjugate, we multiplied out all of the terms in the numerator, because that’s how we get rid of the square root. But we didn’t multiply the terms in the denominator; instead we kept writing it as $x \left(\sqrt{x+5} + \sqrt{5} \right)$. That’s because a few steps later the x canceled.

Something similar will always happen, so in that early step don’t multiply out the part that you didn’t set out to rationalize. Instead just carry those terms along for a while, until you can cancel something. This makes the ensuing algebra much easier.

More practice problems requiring this tactic are waiting for you in Use conjugates to find a limit.

(c) Use Algebra to Find a Limit

\(\displaystyle{\lim_{h \to 0}\dfrac{(h-5)^2 – 25}{h}= ?}\)

As always, we first try Substitution and simply plug $h=0$ into the expression: $$\lim_{h \to 0}\dfrac{(h-5)^2 – 25}{h} \overset{?}{=} \dfrac{(0-5)^2 -25}{0} = \dfrac{25-25}{0} = \dfrac{0}{0}$$ Yet once again, since the limit is in the form   $\dfrac{0}{0},$  it is indeterminate — once again we have more work to do.

In this case, simple algebraic manipulation lets us rewrite the expression into a more helpful form. We have other similar problems for you to try as a tactic on our Use Algebra to Find a Limit screen.

Let’s simply expand the quadratic in the numerator, and then see what happens: \begin{align*} \lim_{h \to 0}\dfrac{(h-5)^2 – 25}{h} &= \lim_{h \to 0}\dfrac{(h^2 -10h + 25) – 25}{h} \\[8px] &= \lim_{h \to 0}\dfrac{h^2 – 10h}{h} \\[8px] &= \lim_{h \to 0}\dfrac{h(h – 10)}{h} \quad \text{[Factor out an $h$]}\\[8px] &= \lim_{h \to 0}\dfrac{\cancel{h}(h-10)}{\cancel{h}} \quad \text{[Ah: cancellation!]}\\[8px] &= \lim_{h \to 0}(h – 10) \quad \text{[We can now substitute]} \\[8px] &= 0 – 10 = -10 \quad \cmark \end{align*} That approach works similarly to the other problems above: the function we started with,  $\dfrac{(h-5)^2 – 25}{h}$, and the one we ended up with after expanding and simplifying,  $h-10$,  are the same except at $h=0.$ The limits of the two expressions at $h=0$ are thus equal.

More Practice and Discussion

Lots more free practice problems for you to try in our Calculating Limits section. There are some other tips and techniques you should know about there too. It’s all free, simply because we believe all dedicated learners deserve access to high-quality materials, and we’d rather you spend your time practicing rather than searching (or having AI develop answers for you, a terrible way to prepare for your actual exams).

If you have questions or thoughts about any limit problem you’re aiming to solve, please let us know either in the Comments below, or better, on our Forum where it’s much easier to write math.

For now, if we’ve helped you learn something, or solidify your understanding, maybe you’d like to add a little fuel to our efforts to develop more material to help students just like you and